О проекте
Курсы
Публикации
Контакты
ЛИЧНЫЙ КАБИНЕТ
Логотип Structuristik
Подкаст
Акции
Подпишитесь на наши новости
Close
ПОДПИСКА НА НОВОСТИ STRUCTURISTIK
Нажимая на кнопку «отправить», вы даете согласие на обработку персональных данных и соглашаетесь c политикой конфиденциальности.
- 30% НА ВСЕ КУРСЫ | Проектируй лето!
промокод DESSUM
Надежда на Надежность

«Конструирование — это искусство придания материалам, которые мы не до конца понимаем, форм, которые мы не можем точно проанализировать, так чтобы они несли нагрузку, которую мы не можем точно спрогнозировать, и при этом у общества не было причин подозревать о масштабах нашего невежества»

Инж. Браун

Введение
Сегодня поговорим о предсказаниях. И если Вы думаете, что предсказания это не для инженеров, то посмотрим, что вы скажите после прочтения материалов.)
Краткая историческая справка
Ни для кого не секрет, что до начала XX века расчет строительных конструкций выполнялся по методу допускаемых напряжений. Все мы выполняли расчеты по этому методу в ВУЗах на курсе Сопротивления материалов. С ним всё просто
Суть проверки заключается в том, что ни на одном участке сечения не должно возникать напряжений больших, чем допустимые. Допускаемые напряжения были указаны в нормативных документах и справочниках в виде таблиц и определялись по формуле:
Коэффициент запаса γ в отдельные промежутки истории мог достигать четырех! Крутое было времечко, наверно. Но если сейчас кто-то скажет вам «Вот раньше строили — века стояло», теперь Вы точно знаете почему.)

С методом допускаемых напряжений, однако, было пару проблем:
  1. Единый коэффициент надежности никак не учитывал ни условия работы конструкции, ни характер напряженного состояния, ни расчетный срок службы сооружения;
  2. Если для сталей сходимость результатов экспериментов и расчетов была удовлетворительна, то для набиравшего популярность железобетона сходимость была просто никудышной. И тогда был предложен метод предельных усилий.
Метод предельных усилий предполагает сравнение не напряжений на наиболее напряженном участке сечения с предельно допустимыми, а действующих усилий с разрушающими, полученными на основе опытов.
Разумная сходимость расчета железобетонных элементов с экспериментами была достигнута, но суть поменялась мало — всё ещё один коэффициент запаса. В СССР и Европе эту проблему понимали и потому исследовались, разрабатывались и предлагались другие методы расчета строительных конструкций.

Удивительно, но метод допускаемых напряжений до сих пор применяется для расчета стальных строительных конструкций в США в качестве одного из методов.

Начало XX века вообще было богато на исследования этого вопроса. В 1926 году Макс Майер показал случайную природу коэффициента надежности, а в 1929 году Николай Федорович Хоциалов предложил метод расчета «по допустимой вероятности разрушения». Основную формулу этого метода можно представить в виде:
То есть вероятность разрушения должна быть меньше предельно допустимой вероятности разрушения. С такой формулировкой метод был обречен на провал. Советским чиновникам, далеким от математики, да и вообще науки, была не понятна формулировка «допустимая вероятность разрушения». Считалось, что вероятность должна быть равна нулю. Буквально «Советский гражданин должен был находиться в зданиях и сооружениях в абсолютной безопасности».

Пусть для нас с вами сейчас это кажется абсурдом, но положение дел, с тех пор, изменилось мало. Так на одном из докладов размещенных на эту тему на YouTube канале AISC упоминается, что Министерство Обороны США считает, что целевой показатель надежности зданий военного назначения должен быть не менее шести сигм. Если Вы пока не понимаете, что это значит, то чуть позже я расскажу подробнее.

Пусть предложение Н. Ф. Хоциалова было раскритиковано. Однако идеи Н. Ф. Хоциалова не были забыты и благодаря трудам Н. С. Стрелецкого, А. Р. Ржаницына, И. И. Гольденблата, В. В. Болотина, В. А. Балдина, В. М. Коченова, М. Я. Пильдиша, К. Э. Таля и других были восстановлены и получили дальнейшее развитие. А чтобы чиновники не пугались страшных слов методу дали новое название — вероятностный метод расчета.

Все мы помним как проходил курс теории вероятности в рамках высшей математики в ВУЗах. Лично я почти ничего не понял. В наших учебных заведениях и литературе принято подавать информацию так, словно слушатель и читатель уже знаком с сутью излагаемых понятий и всё что нужно — написать формулы, по которым всё это вычисляется.

Нет ничего удивительного в том, что предложенный первоначально вероятностный метод расчета был негативно воспринят инженерным сообществом. Сложность расчета возросла в разы и большая часть инженеров, впрочем как и сейчас, была попросту не в состоянии его применять, кроме того банально не хватало статистического материала. Тогда было предложено гениальное компромиссное решение: заменить все вероятностные зависимости детерминированными (определенными) значениями, полученными на основе статистической оценки. По сути, научные институты взяли на себя задачу сбора и обработки статистического материала, а для инженеров оставили почти ту же задачу, что и раньше, обличив статистические зависимости в форму частных коэффициентов надежности.
Кроме того, неотъемлемой частью метода стало понятие предельного состояния. Именно переход от единственной проверки разрушения к набору возможных предельных состояний дал название — «Метод предельных состояний». Позже в нормы ЕС метод вошел под названием «Метод частных коэффициентов надежности», отражая скорее математический аппарат, чем суть самого метода. На данный момент специалисты в теории надежности разделяют понятия «Метод предельных состояний» и «Система частных коэффициентов надежности», но для советских инженеров они вошли в нормы одновременно и не было смысла в их разделении. Метод предельных состояний и сейчас применяется на территории РФ, а также США, ЕС, Канады, КНР, Японии и других стран. Давайте разберемся в статистической природе этого метода, понимая под ним в данной статье скорее систему коэффициентов надежности, чем набор предельных состояний. Для этого нам потребуется освежить в памяти отдельные сведения из теории вероятности.
Комикс о теории вероятности
Природные процессы по своей сути — случайны. Как бы мы не старались и не высчитывали теоретические значения, на практике нагрузки, прочность, условия работы, неточности монтажа и другие факторы хоть и будут находится вокруг какого-то ожидаемого значения, всё равно будут иметь некоторый разброс. Для того чтобы описать разброс математиками было предложено множество законов распределения. Самый часто приводимый в пример — закон распределение Гаусса или закон нормального распределения. Аналитически он записывается так:
От таких формул я невольно поеживаюсь. Ума не приложу как именно Гаусс получил эту формулу. Отсюда и далее я буду делать акцент на графическом представлении материала. Хоть он и имеет существенную условность, но качественно он кажется мне нагляднее и лучше формирует представление о теме. Иногда будут появляться формулы, просто чтобы Вам не пришлось искать их на просторах интернета.

Графически закон нормального распределения выглядит так:

Рисунок 1 — Кривая нормального распределения

По горизонтали отложены значения некоторой случайной величины, а по вертикали вероятность «выпадения» этой величины. По графику видно, что есть некоторая величина посередине, вероятность которой больше, чем у всех остальных — эту величину математики называют «математическим ожиданием» и определяют её по формуле:
В стороны от математического ожидания расходятся две ниспадающие кривые — ветви. Чем дальше значение в обе стороны от математического ожидания, тем меньше вероятность «выпадения» такого значения. Одной из характеристик любого распределения является — стандартное отклонение — его определяют по формуле:
Этот параметр характеризует разброс значений случайной величины и графически выражается в пологости кривой распределения. На рисунке ниже представлены кривые при стандартных отклонениях 0.50, 0.75 и 1.00. Чем больше стандартное отклонение, тем более полога кривая и тем выше разброс значений случайной величины от математического ожидания.

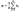
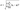
Рисунок 2 — Кривые нормального распределения с различными стандартными отклонениями

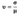
Чтобы вести речь в безразмерных величинах прибегают к ещё одному параметру – коэффициенту вариации. Его определяют по формуле:
По сути — отношение стандартного отклонения к математическому ожиданию. Логика та же — чем больше значение коэффициента, тем больше разброс значений. Так для графика представленного выше коэффициенты вариации составляют 0.050, 0.075 и 0.010 соответственно.

Этот график удобен ещё кое-чем. Площадь под кривой на заданном промежутке значений равняется обеспеченности величины. Обеспеченность — вероятность попадания случайной величины в заданный интервал. Математики часто измеряют обеспеченность в стандартных отклонениях. Так в соответствующей литературе часто встречаются упоминание обеспеченности в одна, две и три и более сигм. Обеспеченность составляет соответственно 0.6827, 0.9545, 0.9973 для одной, двух и трех сигм соответственно, что графически выглядит так:

Рисунок 3 — Обеспеченность одной, двух и трех сигм

По сути это означает, что «выпавшее» значение реальной величины с вероятностью в чуть более 68% попадает в промежуток μ±σ, с вероятностью чуть более 95% попадет в интервал μ±2σ и с вероятностью почти 100% попадет в интервал от μ±3σ. Вычисляется это с помощью интегрирования уравнения закона распределения на заданном интервале. Мне тут запретили писать интегралы, так что просто представьте себе эту формулу, если хотите)

Думаю, теперь Вы понимаете, насколько абсурдно требование обеспеченности параметров в шесть сигм. Практически это означает обеспеченность 0.99 999 999 803. Даже с самыми совершенными процедурами контроля достичь таких значений обеспеченности параметров совершенно невозможно, не говоря уже о том, что при проектировании мы вынуждены работать с ветровыми, снеговыми и другими климатическими нагрузками. Природа, как все мы знаем — не любит соответствовать строгим математическим законам.

Все это, конечно, очень интересно, но как это связано с методом предельных состояний? Дело в том, что в методе предельных состояний в качестве нормативных и расчетных значений как раз и взяты значения величин с определенной степенью обеспеченности. Так в качестве нормативных сопротивлений материалов приняты значения прочности с обеспеченностью 0.95, а в качестве расчетных с обеспеченностью 0.999. То есть из 1000 испытанных образцов, только 50 продемонстрируют прочность ниже нормативной и только 1 окажется менее прочным, чем принято в расчет. Тут появляется первая подсказка: чем меньше коэффициент надежности по материалу, тем надежнее материал сам по себе, и тем ближе к нормативному значению фактическая несущая способность. Так для стали с коэффициентом надежности по материалу γm=1.05 фактическая прочность материала ближе к расчетной, чем для бетона с коэффициентом надежности γm=1.30. То есть фактический запас прочности для бетона выше, чем для стали при одних и тех же коэффициентах использования, а значит и надежность бетонной конструкции выше, чем стальной.

На первый взгляд может показаться, что стоит проектировать больше железобетонных зданий, так как их надежность выше. Но важно понимать, что это вынужденное повышение надежность. Фактические характеристики бетона настолько непредсказуемы и так зависимы от составляющих, технологии приготовления, условий доставки, качества монтажа и ухода, что подчас соседние участки одной и той же железобетонной конструкции могут обладать совершенно различной фактической несущей способностью. Из-за этого приходится существенно занижать расчетные сопротивления бетонов, что приводит к перерасходу материалов и трудовых ресурсов.

Для нагрузок все наоборот. В качестве нормативных значений нагрузок, приняты нагрузки с обеспеченностью непревышения 0.95, а в качестве расчетных с обеспеченностью непревышения 0.999. То есть из 1000 квартир, только в одной полезная нагрузка должна оказаться больше, чем принято в расчет. По крайней мере так задумано. Графическое обозначение обеспеченности нормативных и расчетных параметров приведены на рисунках ниже.

Рисунок 4 — Обеспеченность 0.95

Рисунок 5 — Обеспеченность 0.999

Вот и вторая подсказка — чем больше коэффициент надежности по нагрузке (чем больше он отличается от единицы), тем более непредсказуема в самом деле нагрузка. Вот почему для климатических нагрузок приняты такие большие коэффициенты надежности — потому что мы не можем с достаточной точностью прогнозировать их значения.

Стоит отметить, что для ветровых нагрузок в отечественной нормативной документации принимается распределение Вейбулла, а для снеговых — Гумбеля. Покажем для наглядности графики зависимости законов распределения Вейбулла и Гумбеля при различных коэффициентах формы.

Рисунок 6 — Распределение Вейбулла

Рисунок 7 — Распределение Гумбеля

Забудем пока об отличиях в законах распределения и будем считать, что все нагрузки и все прочностные свойства подчиняются нормальному закону распределения. Тогда метод предельных состояний можно можно изобразить графически в виде двух графиков — кривой нагрузочного эффекта слева и кривой несущей способности справа.

Обратите внимание на то, что речь идет именно о нагрузочном эффекте, а не о нагрузке и несущей способности, а не прочности материала. Благодаря этим переходам мы учитываем условия нагружения и работы элементы, отклонения в размерах сечений и другие параметры несущей конструкции.

Рисунок 8 — Распределение нагрузочного эффекта и несущей способности

Конструкция с коэффициентом использования 1 — идеально запроектированная конструкция — получается когда мы совмещаем значение нагрузочного эффекта с обеспеченностью 0.999 со значением несущей способности с обеспеченностью 0.999. Вероятность отказа равняется площади под пересечениями ветвей этих кривых — та самая ωf вероятностного метода Н. Ф. Хоциалова.

Рисунок 9 — Вероятность отказа идеально запроектированной конструкции

Вероятность отказа может быть определена по формуле:
Здесь ωL — вероятность, что нагрузочный эффект окажется больше расчетного; ωR — вероятность, что несущая способность окажется меньше расчетной. Так как обе эти величины тоже интегралы, то будем считать, что их вид для вас очевиден. Псс, если нужен вид этих интегралов — напишите мне в TG).

Отказ наступает, если несущая способность конструкции оказывается меньше эффекта нагрузки. В остальных случаях, конструкции, которые не достигли отказа, обладают резервом прочности. Согласно А. Р. Ржаницыну резерв прочности может быть определен по формуле:
Волнистые линии над буквами означают случайную величину. Так R означает случайную величину несущей способности, а L означает случайную величину нагрузочного эффекта.

Если резерв прочности больше нуля, то конструкция находится в области допустимых состояний. Проблема в том, что это двухпараметрическая случайная величина и закон её распределения нужно представлять в трехмерном пространстве.

Рисунок 10 — Резерв несущей способности

Здесь оси в горизонтальной плоскости представляют собой величины нагрузочного эффекта и несущей способности. Работать с трехмерными графиками не очень то удобно, поэтому отсюда и далее будем смотреть на этот график сверху. На поверхности этой фигуры можно выделить линии равной вероятности. Эти линии на виде сверху будут представлять эллипсы. Для удобства иллюстрации я буду изображать их в безразмерном виде — в таком виде они примут форму окружности — частного случая эллипса. Также на виде сверху проведем граничное условие — равенство нагрузочного эффекта и несущей способности. Увы, сделать это в MathCAD я не смогу, поэтому придется рисовать графики в AutoCAD.

Рисунок 11 — Многомерная случайная величина

То что делаем мы при применении метода предельных состояний проиллюстрировано на рисунке слева. То, чем это является в действительности — на рисунке справа. На рисунке справа обозначено расстояние от пика нашего сглаженного конуса до граничного условия — это и есть надежность. В нормах США и ЕС эта величина выражена в стандартных отклонениях, названа «индексом надежности» и обозначена символом β. Зависимость вероятности отказа от величины индекса надежности для нормального закона распределения представлена в табличном и графическом виде:

Таблица 1 – Зависимость вероятности отказа от величины индекса надежности
Индекс надежности при вероятности отказа

Рисунок 12 — Зависимость вероятности отказа от индекса надежности

В нормах США этот график слегка отличается, так как в основе метода LRFD в США приняты логарифмически нормальные законы распределения величин. Отличие незначительные и для логарифмически нормальных, как и для других законов распределения приведенные выше рассуждения остаются верными, но имеют слегка другое графическое представление и значения обеспеченностей.
А в наших нормах?
Интересно, что понятие индекса надежности было введено А. Р. Ржаницыным в 1954 году в работе «Расчет сооружений с учетом пластических свойств материалов», однако в то время банально не хватало ни математического аппарата ни достаточных статистических данных, чтобы адекватно его нормировать. Увы, с уходом Н. С. Стрелецкого, А. Р. Ржаницына, В. В. Болотина, И. И. Гольденблата и других метод предельных состояний в нашей стране так и остался полувероятностным — для нагрузок и прочностных свойств собраны самостоятельные статистические данные и назначены коэффициенты надежности, но с результирующей надежностью здания они параметры остались несвязанными. Шагом в эту сторону стал коэффициент надежности по ответственности, обоснование которого в 1981 году было приведено в статье «Учет ответственности зданий и сооружений в нормах проектирования строительных конструкций» под авторством В. А. Отставнова, А. Ф. Смирнова, В. Д. Райзера, Ю. Д. Сухова. Графически эффект этого коэффициента можно представить так:

Рисунок 13 — Многомерная случайная величина

Можно сказать, что нормы США и ЕС предписывают увеличивать расстояние между ожидаемой несущей способностью и граничным условием, а мы сохраняя расстояние наклоняем прямую граничного условия, тем самым увеличивая расстояние от ожидаемой несущей способности до фактического положения граничного условия. Увы, в РФ на уровне документов не установлен целевой показатель надежности, ни в форме индекса надежности, ни в форме допустимой вероятности отказа. Так об этом пишет автор ГОСТ 27 751 В. Д. Райзер:

«Метод предельных состояний подвел идейную базу под уже существующие надежностные требования, но не сформулировал правил их установления. В результате, многие кардинальные положения современных норм расчета строительных конструкций не имеют общей теоретической базы. Не найти разумного объяснения тому, что надежность сооружений одного и того-же назначения, выполненных из различных материалов, запроектированных по действующим нормам, оказывается различной. Невозможно также сказать, какой уровень надежности требуют нормы проектирования, и должен ли он быть одинаковым для всех сооружений или различаться, а если должен различаться, то в каких пределах и в зависимости от чего.»

Кроме того, так как для каждой случайной величины опыты для сбора статистического материала были проведены независимо, а значит и нормативные и расчетные значения были приняты независимо друг от друга, то они никак не связаны с общей надежностью сооружения. В результате:

«Анализ надежности проектируемых конструкций в предположении их идеальной доработки с точки зрения установления расчетных значений (унификация обеспеченностей расчтеных значений) показывает, что уровень надежности зданий или сооружений одинакового назначения может отличаться в несколько раз. Вполне возможны случаи, когда конструкции сооружений наиболее ответственного класса оказываются менее надежными, чем конструкции менее ответственного класса.»

Так резюмирует положение дел В. Д. Райзер:

«Сложившуюся ситуацию в нормировании правил расчета строительных конструкций можно охарактеризовать следующим образом: у проектировщика практически отсутствует информация, насколько успешно решена им задача нормального функционирования сооружения.»

Исследователи уровня надежности, например, авторы работы «Сопоставление уровней надежности, обеспечиваемых нормами Российской Федерации и Евросоюза» В. В. Надольский, М. Голицки, М. Сыкора, В. В. Тур установили, что индекс надежности стальных конструкций, запроектированных по нормам РФ для восприятия снеговой и полезной нагрузок, в среднем находиться в промежутке β=2.3−2.7, хотя иногда может существенно отличаться. При исследовании вопроса назначении расчетных сочетаний нагрузок Ю. Д. Сухов, рассматривая воздействие снеговой и ветровой нагрузок на стальную конструкции приходит к следующему решению:

«Значения вероятностей в (11) однозначно определяются дальностью отказа β (12). На рис. 1 показаны кривые, представляющие зависимость β(ψg), соответствующие левой части уравнения (11) при различных значениях α. Точки пересечения этих кривых с прямой β=2.7 (это соответствует вероятности в правой части (11) 0.9965) являются решениями уравнения (11).»

Вероятностный метод определения коэффициента сочетаний

постоянной нагрузки с временными — СМиРС — 1985

Ю.Д.Сухов


Ю. Д. Сухов — один из авторов обоснования введения в нормы строительного проектирования коэффициента надежности по ответственности. Можно сделать вывод, что для внутренних исследований в 1985 годах сотрудниками ЦНИИСК им. Кучеренко был принят целевой индекс надежности стальных конструкций β=2.7. Более, никакой информации мне найти не удалось.
А что там за бугром?
США
В США целевые индексы надежности приведены в ASCE 7−22 и их значения, что вполне логично, зависит от характера и величины последствий соответствующего отказа. Именно эти значения заложены при определении коэффициентов надежности ф в американской интерпретации метода предельных состояний и коэффициентов Ω при расчете по методу допускаемых напряжений. Для справки данные приведены в таблицах 2 и 3 ниже.

Таблица 2 — Индексы надежности по ASCE 7−22
Таблица 3 — Категории риска зданий по ASCE 7−22
* Здания и сооружения, содержащие токсичные, высокотоксичные или взрывоопасные вещества допускается относить к более низкой категории риска, если с помощью оценки опасности, описанной в разделе 1.5.3, к удовлетворению Компетентного органа может быть доказано, что выброс веществ соизмерим с риском, связанным с этим риском соответствующей категории.
ЕВРОСОЮЗ
В ЕС индексы надежности приведены в приложении C EN 1990:2023. Для сравнения данные приведены в таблицах 4 и 5 ниже.

Таблица 4 – Целевые индексы надежности и вероятности отказа
Таблица 5 — Классификация классов последствий
Класс последствий принимается по большему.
Чтож, показатели надежности в среднем в США и ЕС выше, чем в РФ. И на первый взгляд, может показаться, что следует ужесточить требования к конструкциям и проектировать более надежные здания и сооружения. Но в действительности назначение целевых коэффициентов надежности должно базироваться на оценке экономической ситуации в стране и статистике аварий на действующих объектах. Так, возможности приобретения жилья на рынках недвижимости США и ЕС неутешительные. Повышение надежности приведет к росту материало- и трудоемкости, а значит росту себестоимости объекта капитального строительства. Хуже того, что почти всегда, строительство ведется за счет кредитных средств, особенно с введением с 1.07.2019 счетов Эскроу, согласно 214-ФЗ, что ещё существеннее увеличивает стоимость. Чем больше увеличиваются затраты на материалы и работы, тем больше итоговую стоимость поднимает банковская система, а значит падает уровень и продолжительность жизни, растет преступность и безработица. Не поняли как это работает? Сейчас расскажу
Слишком безопасно
Очевидно, что стоимость АБСОЛЮТНО ВСЕХ услуг и товаров включает в себя стоимость необходимых зданий и сооружений. Дороже строительство и эксплуатация — выше амортизационные расходы — выше стоимость товаров и услуг — нужно больше зарабатывать — нужно больше работать. Рассмотрим, например, покупку жилплощади. Жилище — базовая потребность человека. Чем больше стоит жилище, тем больше и дольше человеку придется работать, чаще отказывать себе в отдыхе и лечении. Те, кто хотят заработать быстрее решаются на работу во вредных производственных или климатических условиях, например, на вредном производстве или в условиях крайнего севера. Это приводит к росту травматизма и развитию заболеваний, как следствие — росту нагрузки на медицинскую систему. Отдельные люди в погоне за быстрым заработком решаются на преступления, что ведет к росту преступности и соответствующим затратам на безопасность и охрану правопорядка. Затраты на медицинское обслуживание и охрану правопорядка проводятся на средства налоговых поступлений. Растут затраты — растут налоги — падает заработок — растет нагрузка. Это замкнутый круг. В дальнейшем весь этот эффект будем называть уровнем жизни.
Расходы на обеспечение безопасности следуют экономическому закону убывающей полезности. Первоначальное резкое снижение риска обходится сравнительно небольшими затратами, однако с ростом затрат снижение риска замедляется и асимптотически приближается к нулю. Совокупный эффект надежности эксплуатационного риска и социального риска можно проиллюстрировать следующим графиком:

Рисунок 14 — Кривые риск-затраты

Синим показана кривая зависимости риска от затрат на строительство и эксплуатацию. Бирюзовым показан социальный риск, он линейно растет с ростом затрат — стоимости приобретения жилья, товаров и услуг. Красным показан полный риск — сумма эксплуатационного и социального рисков. Поначалу полный риск быстро снижается вторя снижению эксплуатационного риска до определенной отметки, но с замедлением снижения эксплуатационного риска и ростом социального риска, полный риск проходит через нижнюю точку и начинает возрастать, асимптотически приближаясь к кривой социального риска. Видно, что неоправданное повышение надежности конструкции приводит к росту полного риска, а значит неоправданному повышению стоимости жилья, товаров и услуг, и, как следствие, снижению уровня жизни. Таким образом, установлении целевых показателей надежности нам следует руководствоваться не просто надежностью одного отдельного здания, а совокупным средним риском на душу населения. Всё это здорово, но причем тут инженеры?
Коэффициент использования
Не смотря на строгую детерминированность метода предельных состояний, решающее значение имеет принятое проектное решение, а именно коэффициент использования. Увы, изложенные ниже значения будут зависеть от стартовой точки. Давайте примем в качестве стартовой точки β=2.7, это будет означать обеспеченность безотказной работы ~0.9965 и соответствовать коэффициенту использования k=1.000. То есть площади под кривой на интервале от минус бесконечности до μ-2.7σ.
При коэффициенте использования k=1.0 действующий нагрузочный эффект будет равен μ-2.7σ. Тогда при коэффициент использования k=0.5 нагрузочный эффект должен быть в два раза меньше, чем при коэффициенте использования k=1, то есть 0.5*(μ-2.7σ), а при коэффициенте использования k=2, действующий нагрузочный эффект составлять 2.0*(μ-2.7σ). Построим график для отношения вероятностей отказа при различных коэффициентах использования. Для вычислений примем коэффициент вариации несущей способности vR=0.12, что в целом близко к коэффициенту вариации несущей способности стальной балки. Коэффициент вариации нагрузки примем vL=0.25, что примерно соответствует коэффициенту вариации полезных нагрузок, тогда зависимость вероятности ежегодного отказа от коэффициента использования примет вид:
Рисунок 15 — Зависимость ежегодной вероятности отказа

от принятого коэффициента использования

Видно, что ежегодная вероятность отказа конструкции с коэффициентом использования k=0.5 примерно в 9 ниже, чем конструкции с коэффициентом использования k=1.0. А ежегодная вероятность отказа конструкции с коэффициентом использования k=2.0, хоть и более чем в 10 раз выше, всё равно не превышает 4%.

Обращаю Ваше внимание, что хоть это и может звучать, как призыв проектировать конструкции с коэффициентом использования больше единицы – это им НЕ ЯВЛЯЕТСЯ. Это скорее призыв не проектировать конструкции с коэффициентом использования меньше 75%. Однако, если так вышло, что спроектированная кем-то другим, или эксплуатируемая на данный момент конструкция имеет коэффициент использования немного больше единицы, например, k=1.05, а усиление объекта для обеспечения k<1.00 приводит к необоснованному повышению стоимости объекта, или полной невозможности его реализации, то возможно, будет целесообразно согласовать данное отступление с заказчиком. Только не забудьте зафиксировать это отступление документально.

Для большей наглядности сведем данные в таблицу 6. Туда же внесем вероятности отказа конструкций при расчетном сроке эксплуатации Y, определяемые по формуле:
Таблица 6 — Зависимость вероятности отказа от коэффициента использования
Надо сказать что полученные значения вероятностей меня пугают. Почти 16% вероятность отказа конструкции за 50 лет эксплуатации. То есть примерно каждый 6-ой элемент конструкции жилого дома КС-2 должен достичь предельного состояния за расчетный срок службы. Тем не менее, практика эксплуатации зданий и сооружений показывает, что принятые значения коэффициентов надежности обеспечивают приемлемую частоту отказов. Ну или почти приемлемую.
Выводы
Представленный выше материал, хоть и является во многом условными допущениями, всё же позволят нам сделать ряд серьезных и не очень выводов:
  1. Если кто-то говорит вам «всегда так делали и не падало» и «ну стоит же» — значит только то, что конструкция просто ещё не выстояла своё. Такой аргумент стоит применять только к зданиями и сооружениям запроектированным с коэффициентом использования k=1.0 и прослужившим свой расчетный эксплуатационный срок;
  2. Не смотря на то, что принятый в РФ индекс надежности β=2.7 принят довольно низким, относительно зарубежной практики, практика эксплуатации конструкций, запроектированных по нормам РФ показывает удовлетворительную частоту отказов;
  3. Не смотря на имеющийся положительный опыт эксплуатации конструкций, запроектированных по нормам РФ, установление и документальное закрепление целевых показателей надежности проектируемых конструкций (будь то индекс надежности или целевая вероятность отказа) является необходимой основой развития и совершенствования нормативно-технической базы РФ. Без этого невозможно ни развитие вероятностных методов расчета, ни уточнение действующих коэффициентов надежности и сочетаний;
  4. Коэффициент использования k=2.00 не является гарантией отказа конструкции, как и коэффициент использования k=0.50 не является гарантией невозможности отказа. При проектировании следует стремится к коэффициенту использования k→1.00. Ну или хотябы k→0.95;
  5. Важнейшая роль инженерного решения. Мы в подкастах часто упоминали выражение генерального директора CSI Ашрафа Хабибула — «Инженер спасает жизни, каждый раз, когда дует ветер». Но если копнуть чуть глубже, то можно сказать так:

Инженер повышает уровень жизни людей каждый раз, когда проектирует эффективную конструкцию!

Если остались вопросы — пишите их нам в социальных сетях.


Автор статьи:

Блинов Сергей

Инженер-конструктор

    •  
    •  
ПУБЛИКАЦИИ