О проекте
Курсы
Публикации
Контакты
ЛИЧНЫЙ КАБИНЕТ
Логотип Structuristik
Подкаст
Акции
PlayCAD
Подпишитесь на наши новости
Close
ПОДПИСКА НА НОВОСТИ STRUCTURISTIK
Даю согласие на обработку персональных данных.
Новогоднее Комбо возвращается. Скидки до 42 000 ₽
КУПИТЬ КУРСЫ
Удивительная история профлиста
ВВЕДЕНИе
В прошлый раз мы вкратце познакомились сразу с тремя методиками расчета профилированных настилов, представленных в нормах РФ. В этот раз детально сравним методики СП 260.1 325 800 и СП 294.1 325 800.

Большинство конструкторов хотя бы раз считали профлист по методике СП 294.1 325 800 или пособию к СНиП II-23−81* откуда эту методику перенесли в СП 294.1 325 800. Кто-то делал это руками, а кто-то с помощью NormCAD, WebCAD или другого ПО. Найти действующего конструктора, кто считал бы профлист по СП 260.1 325 800 не так то просто, что не удивительно, ведь это стандарт предназначенный для проектирования любых ЛСТК конструкций, а не только профлистов и выделить в нем разделы, необходимые для расчета профлиста отдельная интеллектуальная задача.

DISCLAIMER:
По ходу статьи мы сравним предпосылки, лежащие в основе двух методик и результаты по обеим методикам. Будет много формул и графиков детально вникать в которые совсем не обязательно. Главное тут будет в выводах. Увы, привести выводы без обоснования нельзя — засмеют в узких, но авторитетных кругах. Так что придется тут насыпать формул, типа я умный. Не дайте внешнему виду статьи вас запутать, всё не так уж сложно. Если я смог это написать, значит вы точно сможете это понять.

Усаживайтесь поудобнее, наливайте чаек. Будет душно.
Базовые расчетные предпосылки
Как показано великим и несравненным С. П. Тимошенко, критическая сила, при которой плоская форма равновесия становится неустойчивой и пластинка начинает выпучиваться, имеет наименьшее значение, если пластинка квадратная.
Рисунок 1 —Квадратная пластинка
Для квадратной равномерно нагруженной пластинки, критическая сила на единицу ширины b, согласно С.П. Тимошенко может быть определена по формуле:
где E — модуль упругости материала, в нашем случае стали; μ - коэффициент поперечной деформации; t — толщина пластинки; b — ширина пластинки.

Откуда критические напряжения потери устойчивости равномерно сжатой квадратной пластинки получим делением критической силы Fcr на толщину пластинки t:
где E — модуль упругости материала, в нашем случае стали; μ - коэффициент поперечной деформации; t — толщина пластинки; b — ширина пластинки.

Формула определения критических напряжений потери устойчивости сжатой пластинки в СП 260.1 325 800 имеет вид:
где kσ - коэффициент, учитывающий напряженное состояние пластинки; E — модуль упругости материала, в нашем случае стали; μ - коэффициент поперечной деформации; t — толщина пластинки; b — ширина пластинки.

Коэффициент kσ в формуле учитывает рост критических напряжений по мере увеличения неравномерности нагружения пластинки. Нетрудно догадаться, что для равномерно сжатой пластинки kσ=4. Правила определения коэффициента kσ для других случаев приведены в таблицах 7.2 и 7.3 СП 260.1 325 800 в зависимости от количества закреплений пластинки и коэффициента неравномерности нагружения ψ, который отражает отношение меньших напряжений к большим и может быть определен по формуле:
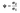
где σ2 — меньшие из напряжений; σ1 — большее из напряжений.

При этом сжатие считается положительным, а растяжение — отрицательным. При ψ=1 пластинка равномерно сжата и kσ=4; при ψ=0 эпюра сжимающих напряжений приобретает треугольный вид, а коэффициент kσ=7.81; при ψ=-1 эпюра напряжений состоит из двух одинаковых треугольников, а kσ=23.9.
Рисунок 2 — Эпюры напряжений для пластин при ψ=1, ψ=0, ψ=-1
То есть пластинка на разных концах которой действуют одинаковые по величине, но разные по знаку напряжения примерно в 6 раз более устойчива, чем сжатая равномерно по всей длине.

В СП 294.1 325 800 формула определения критических напряжений потери устойчивости сжатой пластинки представлена в следующем виде:
где k0 — коэффициент, учитывающий напряженное состояние пластинки; k01 — коэффициент, учитывающий повышение критических напряжений при наличии достаточно высоких напряжений смятия на перпендикулярной грани; t — толщина пластинки; b — ширина пластинки.

Почему я так решил? Эта формула совсем не похожа на формулу С. П. Тимошенко! Давайте докажем их родство:
где E — модуль упругости материала, в нашем случае стали; μ - коэффициент поперечной деформации; t — толщина пластинки; b — ширина пластинки.
Классический пример того, как иногда замудрено могут написать наши нормы. Видимо, чтобы никто не догадался, какие именно предпосылки лежат в основе принятых методик.
В полученной выше формуле отсутствует коэффициент k01, учитывающий повышение критических напряжений при наличии достаточно высоких напряжений смятия на перпендикулярной грани. Логично, что этот коэффициент актуален только для стенок, так как в качестве сминающих напряжений в этом случае выступает опорная реакция на нижней полке профлиста. Для других пластинок его применять не следует. Согласно Б. М. Броуде, коэффициент k01 может быть определен по формуле:
где z — расчетная ширина зоны опирания; h — высота профиля.
И вот тут нужно обратить внимание на числитель первой дроби. Дело в том, что в СП 294.1 325 800 в числители стоит толщина стенки t, но должна стоять расчетная ширина зоны приложения поперечной нагрузки z. Ещё в пособии 1985 года формула была написана верно, но при переносе в СП 294.1 325 800 допустили опечатку. Почему за почти 10 лет и 3 изменения её так и не исправили?
Есть загадки, ответы на которые нам лучше не знать…
Повышающий коэффициент k01 начинает оказывать влияние при z/h≥0.7 и σloc/σ≥0.14. В нормах эта граница поднята чуть выше до z/h>0.9 и σloc/σ≥0.4 в запас надежности.

Коэффициент k0 в СП 294.1 325 800 дан в табличном виде. Сам же коэффициент зависит от отношения длины пластинке к ширине и степени неравномерности нагружения ξ. Согласно методике Е. И. Шкловского коэффициент k0 может быть определен по аппроксимирующей опытные данные формуле:
где ξ - коэффициент, неравномерности нагружения.

Коэффициент неравномерности нагружения ξ, учитывающий напряженное состояние пластинки, Е. И. Шкловским предложено определять по формуле:
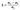
где σc — наибольшие сжимающие напряжения; σt — наименьшие сжимающие или растягивающие напряжения.

Здесь, как и в СП 260.1 325 800 сжимающие напряжения принимают положительными, а растягивающие — отрицательными. Видно, что коэффициент ξ, положенный в основу коэффициента k0 из СП 294.1 325 800 является аналогом коэффициента ψ, положенного в основу kσ из СП 260.1 325 800. Тогда можно установить зависимость между коэффициентами ψ и ξ:
где ψ - коэффициент, неравномерности нагружения по методике СП 260.1 325 800.

Приведем kσ к виду k0 с помощью выражения:
где kσ - коэффициент, учитывающий напряженное состояние пластинки; E — модуль упругости стали [МПа]; μ - коэффициент поперечной деформации.

Тогда с учётом зависимостей между коэффициентами неравномерности нагружения ψ и ξ построим график зависимости коэффициентов k'σ и k0 от коэффициента неравномерности нагружения ξ.
Рисунок 3 — Коэффициенты k0 и k’σ
Видим, что коэффициенты k'σ и k0 имеют существенные расхождения на участке ξ<0.5 (ψ>0.5) и ξ>3 (ψ<-2), что соответствует ситуациям сжатия с небольшим эксцентриситетом и существенного внецентренного растяжения. Это оправдывается тем, что профлист не планировали использовать в качестве центрально сжатых или внецентренно растянутых элементов.
Рисунок 4 — Напряженные состояния пластинки при ψ=0.5 и ψ=-2
Если положение центра тяжести сечения известно, то не составляет труда определить коэффициенты ξ для стенок и, как производное от них, коэффициенты k0, что и сделано для стандартных профлистов в СП 294.1 325 800.
Видим, что в основу методик СП 260.1 325 800 и СП 294.1 325 800 положены одинаковые предпосылки, а разница в величине критических напряжений обусловлена в первую очередь учетом повышения критических напряжений потери устойчивости пластинки при наличии достаточно высоких напряжений смятия на перпендикулярной грани с помощью коэффициента k01.
1:0 в пользу СП 294.1 325 800.
Учет потери устойчивости
После того как напряжения достигают критических сжатая пластинка начинает терять устойчивость, а усилия с участка потерявшего устойчивость перераспределяются на прилегающие участки. В расчетах это учитывают заменяя реальную ширину пластинки b на эффективную ширину beff.
Рисунок 5 — Реальное и эквивалентное распределения напряжений по ширине сжатой пластинки
Как было показано многочисленными экспериментами, эффективная ширина пластинки beff зависит от действующих напряжений и соотношения между шириной b и толщиной t пластинки. Согласно теории Кармана-Винтера эффективная ширина пластинки может быть определена по формуле:
где t — толщина пластинки; b — ширина пластинки; E — модуль упругости стали; Ry — расчетный предел текучести стали.
Вообще, вместо Ry в формуле должны стоять максимальные сжимающие напряжения σc.max, но минимальное значение эффективной ширины полки будет именно при σc.max=Ry и на практике, чаще всего, определяют именно минимальное значение эффективной ширины полки beff несколько в запас, предполагая, что напряжения в крайних сжатых волокнах равняются расчетному пределу текучести. Такое решение не слишком консервативно, но сильно упрощает задачу расчета.
Графики изменения отношения эффективной ширины пластинки beff к толщине пластинки t в зависимости от отношения полной ширины пластинки b к толщине пластинки t для сталей классов прочности 220, 250, 280, 320, 350, 390, 420 и 450 по ГОСТ 14 918–80 представлены на рисунке 6.
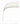
Рисунок 6 — Эффективная ширина пластинки согласно теории Кармана-Винтера
С теоретическим базисом покончено, теперь перейдем к тому, как это учтено в нормативных методиках расчета.
Растянутые пластинки, само собой, устойчивость не теряют. Уверен, вы и сами догадались, но так, чисто на всякий случай, а то видел я уже один учебник по ЛСТК…
Работа полок
СП 260.1 325 800
СП 260.1 325 800 предполагает прямое применение методики Кармана-Винтера. В первую очередь определяется редуцированная гибкость, затем определяем коэффициент редукции, и уже следом определяем эффективную ширину.
Формулы приводить не буду. И так статья перегруженной получается. Потом в формульном отчете PlayDeck посмотрите. Ну или в СП 260.1 325 800 тоже можно.
Хотелось бы сказать, что это всё. Но увы, это не так. Дело в том, что элементы жесткости, пусть они так и называются, не обладают бесконечной жесткостью и тоже теряют устойчивость.
Рисунок 7 — Потеря устойчивость формы сечения полки
Поэтому толщину пластинок элемента жесткости и примыкающих пластинок также редуцируют. Методика определения редуцированной толщины изложена в разделе 7.4.2 СП 260.1 325 800. Всё довольно просто и близко к теории. А что же там в СП 294.1 325 800?
СП 294.1325800
СП 294.1 325 800 не дает указаний по определению эффективной ширины полки beff. Вместо этого приводит таблицу с геометрическими характеристиками профлистов по ГОСТ 24 045–2016, в п. 23.2.2 указано:
«Расчетная ширина плоских участков сжатых полок профилей принимается равной 40t при определении моментов сопротивления и 60t — при определении моментов инерции…
Криволинейные участи, стенки гофров и растянутые полки настила включены в расчетную площадь сечения полностью."

Та же надпись и в примечании 2 к таблицам 1−9 ГОСТ 24 045–2016:
«Данные по геометрическим характеристикам профилей (моменты инерции и сопротивления) являются справочными и получены принятием расчетной ширины b плоских участков сжатых полок равной: b=40t — при определении моментов сопротивления; b=60t — при определении моментов инерции.»

И только в приложениях к первому ГОСТ 24 045–80 есть сопроводительная картинка.
Рисунок 8 — Указания по определению справочных величин ГОСТ 24 045–80
Куда картинка потом делась, как всегда, можно только гадать. То ли бумаги пожалели, то ли просто лень было её перерисовывать…
То есть согласно ГОСТ 24 045–80 и далее и СП 294.1 325 800 эффективная ширина полок постоянна и не зависит ни от соотношения ширины b и толщины t пластинки, ни от действующих напряжений (класса прочности стали). Может просто принято консервативно?

Согласно рисунка 6 по мере роста отношения ширины пластинки к толщине эффективная ширина полки beff рано или поздно достигает 40t. Для профлистов по ГОСТ 24 045–80 минимальное отношение ширины пластинки b к толщине t составляет 48 для профлиста Н60−845−1.0. Таким образом, согласно формуле Кармана-Винтера эффективная ширина полки beff может составлять 40t только для профлистов из сталей классов прочности 220, 250 и 280. Для профлистов из сталей классом прочности 320 и выше эффективная ширина полки beff будет меньше, чем 40t, а значит эффективные геометрические характеристики, приведенные в ГОСТ 24 045–2016 окажутся завышенными.

Кроме того, из рисунка следует, что СП 294.1 325 800, не учитывают потерю устойчивости формы сечения, что является некорректным. Так, для листа Н60−845−0.8, выполненного из стали класса прочности 220 толщина стали на редуцированных участках составляет 0.75 мм, а эффективная толщина элемента жесткости полки и прилегающих к нему участков полки составляет 0.59 мм, что также приводит к уменьшению геометрических характеристик профиля и смещению центра тяжести сечения.
Рисунок 9 — Редукция толщины элемента жесткости и примыкающих участков профиля
Вот только в ГОСТ 24 045–2016, например, отношение b/t для листа Н153−850−1.5 не составляет и 30. При таком отношении сторон согласно рисунка 6 эффективная ширина полки с трудом подбирается к 30t, зато для любого класса прочности стали.
Надо бы, наверно, заводить отдельный счетчик для оговорок применения методики СП 294.1 325 800.
Таким образом принимать геометрические характеристики профилированных настилов согласно ГОСТ 24 045–2016 попросту не безопасно, особенно для профлистов из высокопрочных марок стали.
1:1 — ничья.
Профлисты со стенками без элементов жесткости
СП 260.1 325 800
По стенкам СП 260.1 325 800 предлагает нам два подхода: или рассмотреть стенку как вырезанную пластинку, определить редуцированную гибкость, затем коэффициент редукции и эффективную ширину как и для полок согласно раздела 7.3.1 или сразу рассмотреть ее как стенку по специальным формулам раздела 7.4.3. По крайней мере так выглядит на первый взгляд. На самом же деле формулы раздела 7.4.3 это просто частные приложения общих формул раздела 7.3.1 только вместо beff.1 и beff.2 стоят обозначения sef.1 и sef.2. Не более того.
Разрушающая нагрузка
В связи с особенностями всех трёх методик единственным вариантом для их сравнения я вижу сравнение нагрузок, которые приводят к отказу профлиста по соответствующему стандарту. Рассмотрим 5 типоразмеров профилей по ГОСТ 24 045–2016 со средней для типоразмера толщиной стенки, выполненных из сталей двух классов прочности: 250 и 320. Все профлисты считаем изготовленными из проката по ГОСТ 14 918–2020. Полученные 10 расчетных схем сведем в таблицу 1.
Честно сказать сам я вторым способ не считал ни разу. Выглядят результаты похоже, так что уверен, что отличия между обоими подходами будет не большая.
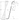
Рисунок 10 — Редукция сечения стенки
Критическая поперечная сила потери устойчивости стенки при приложении поперечной нагрузки согласно СП 260.1 325 800 может быть определена по формуле:
где γc — коэффициент условий работы; C, Cr, Cb и Ch — коэффициенты, определяемый по таблица 8.7−8.11; t — толщина стенки; Ry — расчетный предел текучести стали; φ - угол между плоскостью стенки и плоскостью опорной поверхности; r — внутренний радиус гиба; b — ширина опоры; h — высота плоской части стенки профиля.

Видим, что критическая поперечная сила потери устойчивости стенки Qw.p зависит от способа закрепления (учитывается коэффициентами С, Cr, Cb, Ch), толщины стенки t, расчетного предела текучести стали Ry, угла между плоскостью стенки и плоскостью опорной поверхности φ, радиуса скругления между полкой и стенкой r, ширины опоры b и высоты профиля h. 

Тут, вроде, всё понятно. Смотри размер, подставляй и считай. Проще некуда.
СП 294.1325800
Теперь переходим к отечественному БДСМ с элементами акробатики. Помним, что согласно п. 23.2.2 СП 294.1 325 800 и примечаний к таблицам ГОСТ 24 045–2016 устойчивость стенок должна быть обеспечена.

То есть если при проектировании по СП 260.1 325 800 мы допускали местную потерю устойчивости стенок и определяли несущую способность с этим учетом, то при проектировании по СП 294.1 325 800 мы выбираем профлист так, что бы устойчивость стенок профлистов была обеспечена.

Для элементов без «уступов» на стенках СП 294.1 325 800 приводит следующую зависимость:
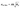
где A — коэффициент, неизвестной пока природы, определяемый по таблице 60; k — коэффициент, неизвестной пока природы, определяемый по таблице 61; Ry — расчетный предел текучести стали [МПа].

И сразу два не пойми откуда взявшихся коэффициента A и k. Ноги этих коэффициентов растут всё из той же диссертации Е. И. Шкловского, согласно которой по результатам испытания 646 образцов критические напряжения смятия при загружении полки сосредоточенной нагрузкой на промежуточной опоре могут быть определены по полученной методом корреляционно-регрессионного анализа формуле:
где d — ширина опоры [мм]; r — радиус скругления между полкой и стенкой [мм]; h — высота профиля [мм]; t — толщина стенки [мм]; Ry — расчетный предел текучести стали [МПа].
Пусть слова «корреляционно-регрессионный» анализ вас не пугают. Да, Ефиму Исааковичу пришлось изрядно потрудится подбирая коэффициенты регрессии, но каждый из нас сейчас может открыть Excel, вставить результаты испытаний в табличку, построить график и линию тренда. Уравнение, описывающее линию тренда и будет нужным вам уравнением. Если есть желание, можно даже вбить результаты испытаний из диссертации и подобрать уравнения поточнее. Впрочем, вы этим никому ничего не докажите)
Так что же мы видим? Внешний вид зависимости другой, но учитываемые факторы те же! Ну или почти те же. В отличие от СП 294.1 325 800 в методике СП 260.1 325 800 учитывается ещё и угол наклона стенки к опорной поверхности φ. Кроме того коэффициенты C, Cr, Cb и Ch учитывают наличие прикреплений к опоре (подвижность опоры), количество сил, приложенных к профлисту и тип опоры (промежуточная или концевая).

Строго говоря, в диссертации Е. И. Шкловского есть аналогичная формула и для определения критических напряжений на концевой опоре, но в текст пособий и СП 294.1 325 800 она не вошла. Если вдруг кому надо, то вот она:
где d — ширина опоры [мм]; r — радиус скругления между полкой и стенкой [мм]; h — высота профиля [мм]; t — толщина стенки [мм]; Ry — расчетный предел текучести стали [МПа].

Так как формула критических местных напряжений на крайней опоре в СП 294.1 325 800 и пособие к СНиП II-23−81* не вошла, то рассматривать будем соответствующую зависимость для критических местных напряжений на промежуточной опоре. Если потребуется, вы без труда сможете сделать тоже самое и для крайней опоры.

Проще всего тут с коэффициентом, учитывающим ширину опоры. В СП 294.1 325 800 он назван k и дан в табличном виде. Аналитически коэффициент k для промежуточной опоры может быть определен по формуле:
где d — ширина опоры [мм].
Рисунок 10 — Зависимость коэффициента k от ширины опоры
В целом, интерполяция по табличным значениям дает отличную сходимость. Формула пригодится разве что, если ширина опоры выходит за пределы таблицы или удобнее реализовать расчет в математическом пакете без интерполяции. И, да, опоры шириной 20 и 240 мм входили в исследование.
Логично предположить, что все остальные члены формулы, кроме корня из предела текучести стали Ry, свернуты в коэффициент A. Тогда, коэффициент A для промежуточной опоры должен определяться по формуле:
где r — радиус скругления между полкой и стенкой [мм]; h — высота профиля [мм].

Увы, это не совсем так. Так как изначальная зависимость является результатом статистической обработки и все величины в нее подставляются без размерностей, то нужно ввести еще два поправочных коэффициента и формула для определения коэффициента A приобретает следующий вид:
где r — радиус скругления между полкой и стенкой [мм]; h — высота профиля [мм]; t — толщина стенки [мм]; g — ускорение свободного падения [м/с2].

Подставим в полученную формулу данные для профлистов Н57−750 и Н60−845 по ГОСТ 24 045–2016 и сравним с данными, приведенными в СП 294.1 325 800. Результаты представлены в таблице 1.
ПУБЛИКАЦИИ